In a previous post we saw that sound is made up of waves of differing pressure in the air, caused by the vibration of air particles. Musical sounds are no exception – even the most intricate and exquisite chords are still encoded in the back-and-forth motion of the air particles that carry the wave from source to ear. What is it that makes some vibrations sound musical, while others sound like speech, or noise? In this three-part series, we’ll look at what makes up a musical sound. I’ll start in part 1 by explaining the basic physical quantities defining a sound wave, and how they relate to more familiar properties of a musical sound – its pitch and loudness.
Loudness
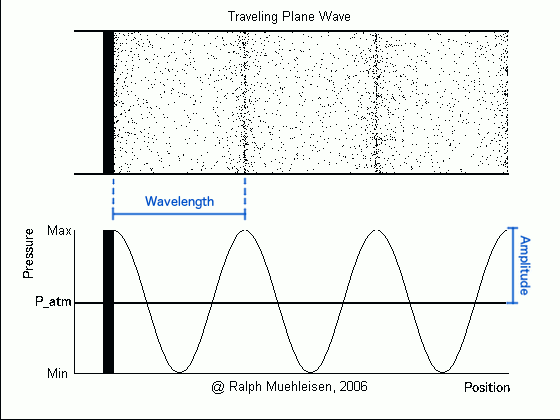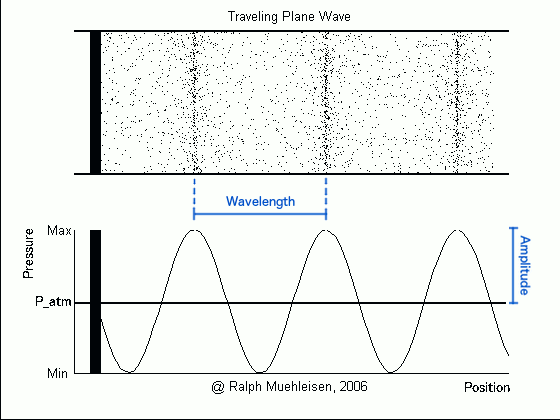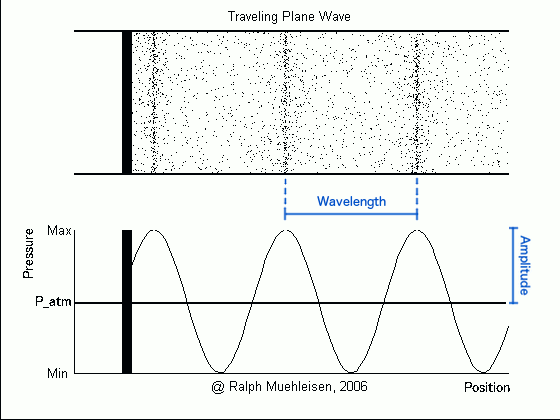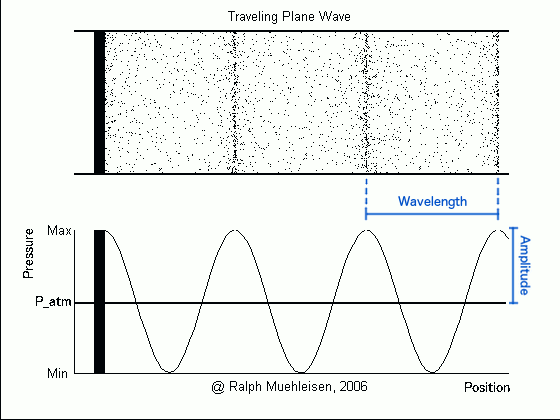
Consider again this animation of sound waves, paying particular attention to the plot of pressure against position at the bottom. The horizontal line in the plot shows the average atmospheric pressure, while the wave traces out the pressure at a particular point in space at a particular time – this pressure can be higher or lower than the atmospheric pressure. The difference between the highest pressure (at the wave crests) and the average pressure is called the pressure amplitude of the wave.
A larger pressure amplitude corresponds to a louder sound. This makes sense – if the piston (or loudspeaker membrane, or other vibrating object) that is producing the sound wave is pushing more on the air particles, they will cluster closer together at the compressions and be spread further apart at the rarefactions, so that the difference between the highest and lowest pressures is greater. When the pressure wave (i.e. the sound wave) hits our eardrum, the eardrum would in turn vibrate more, making the sound sound louder.
Click to Expand: Measuring Loudness in DecibelsIn discussing sound waves, another oft-quoted physical quantity is the intensity of the wave, which measures how much energy the wave carries across a unit area in a unit time. The intensity is proportional to the square of the pressure amplitude:
How does sound intensity relate to loudness? It turns out that our ears perceive loudness on a logarithmic scale – each time the intensity of a sound is doubled, it sounds like it got louder by the same amount. This is why we usually measure loudness on the decibel (dB) scale – this is a logarithmic scale for which each doubling of intensity corresponds to an increase in loudness of about 3 dB. The technical term for this decibel-based measure of loudness is sound pressure level, or SPL. For the mathematically-inclined,
where 
. The constants in this equation were chosen such that 0 dB corresponds to a barely audible sound, and 130 dB to a painfully loud one. A normal conversation is about 60 dB, while a rock concert could subject your ears to 120 dB – that’s 
, or about a million, times more energy than a conversation has!
The decibel scale is also used to measure sound levels in digital music files, or energy levels in sound systems. In these applications, the scale is normalised differently, so that 0 dB corresponds to the loudest sound the system can handle (without clipping or blowing out). We therefore usually see negative decibel values when looking at the meters on audio software.
Click to Expand: Do Two Trumpets Sound Twice as Loud as a Single One?
Short answer:
No, or we would all go deaf when listening to a brass band!
Long answer:
When we double the number of trumpets, it is the sound intensity that doubles. (This makes sense, since the intensity measures the amount of energy carried by the wave in a unit time across a unit area. Two trumpeters should produce twice the amount of energy per second as one player, and the area through which the sound waves are passing is the same if the listener is standing in the same location with respect to the trumpeters.) Therefore, two trumpeters should sound 3 dB louder than one player, while a band of 20 brass instruments would be 13 dB louder than one trumpeter (making the coarse approximation that each instrument is equally loud).
Readers who have studied waves in physics or engineering classes might wonder why the sound waves from the two instruments don’t add constructively, leading to a wave of double the amplitude and quadruple the intensity. Or why, for that matter, don’t they interfere destructively, leading to no sound at all? Why do we not get an interference pattern in space, so that you hear nothing in some spots and a really loud sound in others?
There are several reasons for this lack of interference. Firstly, the two sources are not coherent, meaning that they do not have a constant phase difference. (A string player playing vibrato, for instance, constantly changes the phase and frequency of their note.) Secondly, real musical instruments rarely produce pure tones of a single frequency – instead, each note is made up of many harmonics. The strength and phase of each harmonic differs between the two instruments. So while it may be possible to have one harmonic cancel out at one spot at a certain point in time, the other harmonics would still be heard, and usually the effect is too transient to be noticed. Furthermore, in many rooms the sound that you hear comes not just directly from the musicians, but also from reflections (possible multiple ones) off the walls, further blurring out any interference effects.
That said, in some artificial circumstances you can create interference between two sound sources. Try it with two speakers connected to the same source, playing a pure sinusoidal tone – if you walk in a straight line parallel to the line connecting the speakers, you might hear the sound alternately getting louder and softer. Check out this link for a demo.
Pitch
Imagine placing a counter at a particular point in space, counting the number of pressure crests that pass by each second as a sound wave travels through the air. This number is the frequency of the wave. The frequency is also equal to the number of times per second a vibrating air particle makes a full back-and-forth motion. Frequency is typically measured in units of Hertz (abbreviated as Hz) – one Hertz corresponds to one cycle per second. The human ear can hear sounds with frequencies ranging from 20 Hz to 20000 Hz.
The frequency of a sound is closely related to the pitch that we hear – a higher frequency (i.e. faster vibration) corresponds to a higher pitch. To be more specific, doubling the frequency of a sound makes it an octave higher. (For the mathematically-inclined: frequency and pitch are logarithmically related, just like amplitude and perceived loudness.) The perceived interval between two musical notes, therefore, is determined by the ratio of their frequencies. For instance, a frequency ratio of 2:1 is an octave, while a ratio of 3:2 is a perfect fifth. Exactly how we define musical intervals based on frequency ratios has been a matter of contention for centuries – one that I’ll talk about in a future post.
Have a listen to the following extract of Twinkle, Twinkle Little Star, played twice. Though the second version is in a higher key (has a higher starting note), both versions are clearly recognisable as the same tune:
When we hum a melody or hear a tune that we recognise, it is the frequency ratios between successive notes, and not the absolute frequencies of each note, that matter. A male singer may choose to sing a song in a lower key than a female vocalist, but as long as the musical intervals between successive notes (and the rhythm, of course) are the same between the two singers, the tunes will be recognisable as the same.
For the sake of standardising things so that many musicians can play together, people have developed definitions of absolute pitch. In western music, for example, each note on the 12-tone scale has a name and a specific frequency. The current standard is defined such that the A above middle C has a frequency of 440 Hz. Middle C itself has a frequency of 261.63 Hz. You can find a handy chart here that shows you the frequency of each note in an 8-octave range. (The number after the note letter tells you which octave the note is in, with larger numbers corresponding to higher octaves. Middle C is C4, and the A above that is A4. A standard 88-key piano has a range of A0 to C8.)
Click to Expand: The Meandering Path to the A = 440 Hz Pitch StandardBefore the 19th century, there was no effort to standardise pitch definitions across Europe, and the frequency used for the same letter note could vary by as much as 5 semitones (a frequency difference of 30%). The choice of pitch was sometimes made for reasons of convenience – church organs, for example, are tuned by hammering the top ends of the organ pipes so that they bend inwards or outwards. When this wear-and-tear sustained over the years became too much, people simply cut off the tops of the pipes and started again, raising the overall pitch of the organ!
Pitch standards also had a tendency to rise over time, a phenomenon known as pitch inflation. This occurred because listerners preferred the brighter, louder sounds of instruments tuned to higher pitches. Singers, however, found themselves experiencing throat strain while attempting to keep up with these ever-increasing frequencies. Their lobbying led the French government to pass a law which set the frequency of A above middle C to be 435 Hz – this pitch definition was known as the diapason normal (diapason is the French word for “tuning fork”). Despite this standard, and others set by international conventions (including an article in the Treaty of Versailles!), pitch definitions continued to vary across orchestras – as can be heard in this video which collects the opening chords of Beethoven’s Eroica, played by various orchestras from 1924 to 2011.
While A = 440 Hz is the currently used pitch standard, some orchestras still tune higher, to 442 or even 445 Hz. It is also common for baroque ensembles to use lower tunings, to obtain the warmer sound characteristic of that time period.
The human ear is remarkably good at discerning small changes in frequency (down to 1-2 Hz). While we could never describe, just by listening alone, exactly how much louder one sound is than another, a trained musician can easily tell if the interval between two notes is even slightly out-of-tune. This is a rather interesting ability, given that (as far as I know) there doesn’t seem to be any evolutionary advantage to being able to discern pitch so precisely.
In computer software, we often see music represented as a waveform:
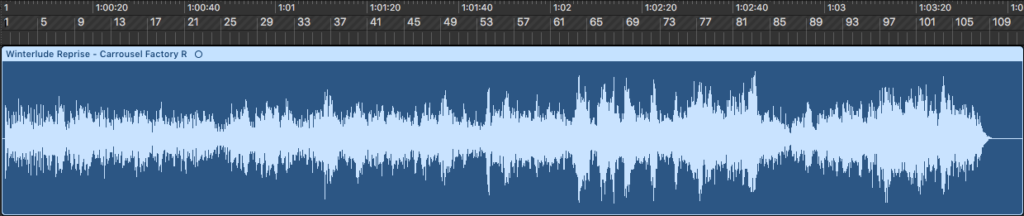
If we zoom in on a small stretch (about 100 milliseconds) of the above waveform, we can see the individual curves of the wave:
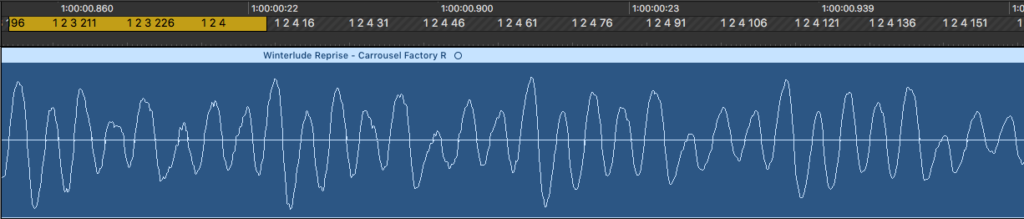
The waveform is actually just a plot of pressure against time (note the time ticks on the topmost horizontal ruler). It might be easy to confuse this waveform with the moving pressure wave that we saw in the animation at the beginning of this post, but while both of them show pressure on the vertical axis, their horizontal axes are different. The animation shows pressure plotted against position on the horizontal axis. For the waveform, however, we assume that our position is fixed, and the plot shows how the pressure at a particular point in space changes as a function of time. When a song is played on a speaker, the vibrations of the speaker membrane follow the undulations of the song’s waveform.
This particular zoomed-in section happens to be part of a ukulele chord plus bass guitar note. The waveform is periodic, which means that the pattern of pressure variations in the wave repeats itself after a fixed amount of time. In this case, the section marked by the yellow bar roughly repeats itself 4 times in the pictured segment. In general, a musical note with a pitch has a periodic waveform, while the waveform of an unpitched sound (such as a hand clap) would not be particularly periodic.
Wavelength
There is one more important quantity that is often used when studying waves. This is the wavelength, or distance between successive crests (or compressions) of the pressure wave.
Wavelength and frequency are inversely related – if you double the frequency of a wave, its wavelength must be halved:
.
In air, the speed of sound is 343 metres per second. A middle C note with frequency 256 Hz would thus have a wavelength of 1.17 metres. Wavelengths of audible sound waves range from 1.5 centimetres to 15 metres. These wavelengths could be an important consideration in designing speakers, concert halls, and musical instruments, since the dimensions of these objects determine at which pitches they resonate best.
We’ve looked at the basic properties of a musical sound – its amplitude, frequency and wavelength. In the next post I’ll move on to talk about the more complex property of timbre, which allows us to distinguish notes played by different instruments, and between the voices of different people.
Leave a Reply
1 Comment on "What Makes a Musical Sound Part 1 – Pitch and Loudness"
Please contact me about a request to license the Traveling Plane Waves animation by Ralph T. Muehleisen for use in an educational context.