The Fourier Transform and the Spectrum

In What Makes a Musical Sound Part 2, I talked about the spectrum, which shows what frequencies are present in a sound.  In this explicative post, I’ll go into more detail about how we obtain the spectrum, and about what it means when we say a sound is made up of different frequencies.

Sine Waves

But first – what does it mean when a sound has a frequency of, say, 784 Hz?  Well, it means that its waveform is periodic and repeats itself 784 times per second.  But this tells us nothing about the actual shape of the waveform.  It could look like this:

Or this:

Or this:

In each of the above cases, the highlighted part repeats itself every 1/784th of a second.

Which of the above is the most natural-looking wave?  You would probably have chosen the third case, since it’s nice and smooth.  This is a sine wave, and we see it often in nature.  For example, if we were to suspend a weight on a spring, and then pull it down and release, the weight would oscillate up and down, and its height as a function of time would trace out a sine wave:

Harmonic Oscillation HD by Alexander C.

Or, if we had a spinning wheel, and focus on a point on the circumference of the wheel, then the vertical position of that point as a function of time would trace out a sine wave:

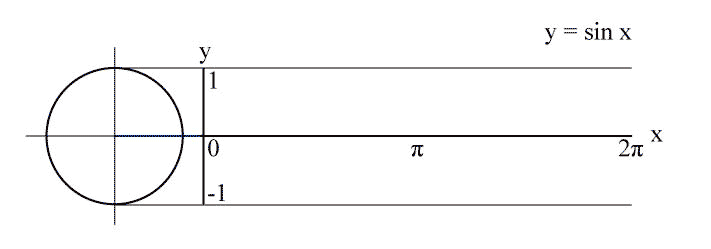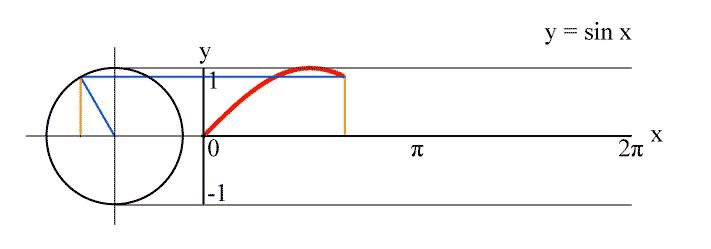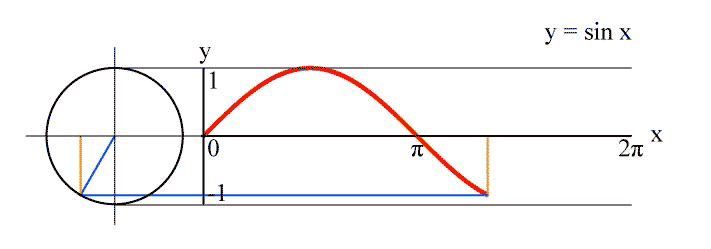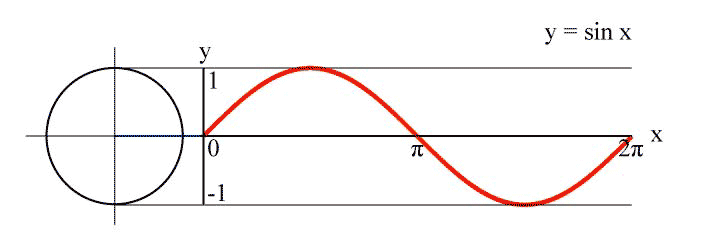
What about sound waves?  Consider the tuning fork, which is an instrument used to provide a reference pitch (because its natural vibrating frequency is not too much affected by things like temperature and humidity, unlike other instruments).  You use a tuning fork by striking it against an object, usually one that isn’t too hard (such as your wrist).  This sets its split ends, or tines, vibrating.  If we followed the position of the tip of one of the tines, it would trace out a sine wave as a function of time.  The tines in turn push on the surrounding air particles, causing them to also vibrate sinusoidally (in a sine-like manner).  You can see a tuning fork vibrating in this slow-motion video:

Tuning Fork Vibration by Dan Russell.

However, most other musical sounds are more complex.  A violin string vibrates in a more complicated pattern than a simple sine wave, and so in turn do the air particles which are set in motion by the instrument.  Have a look at the following waveform, which is a small fragment of a violin note playing at 784 Hz (the note G5).  The segment marked by the braces repeats itself every 1/784th of a second.

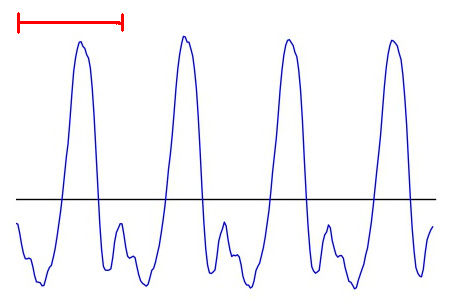
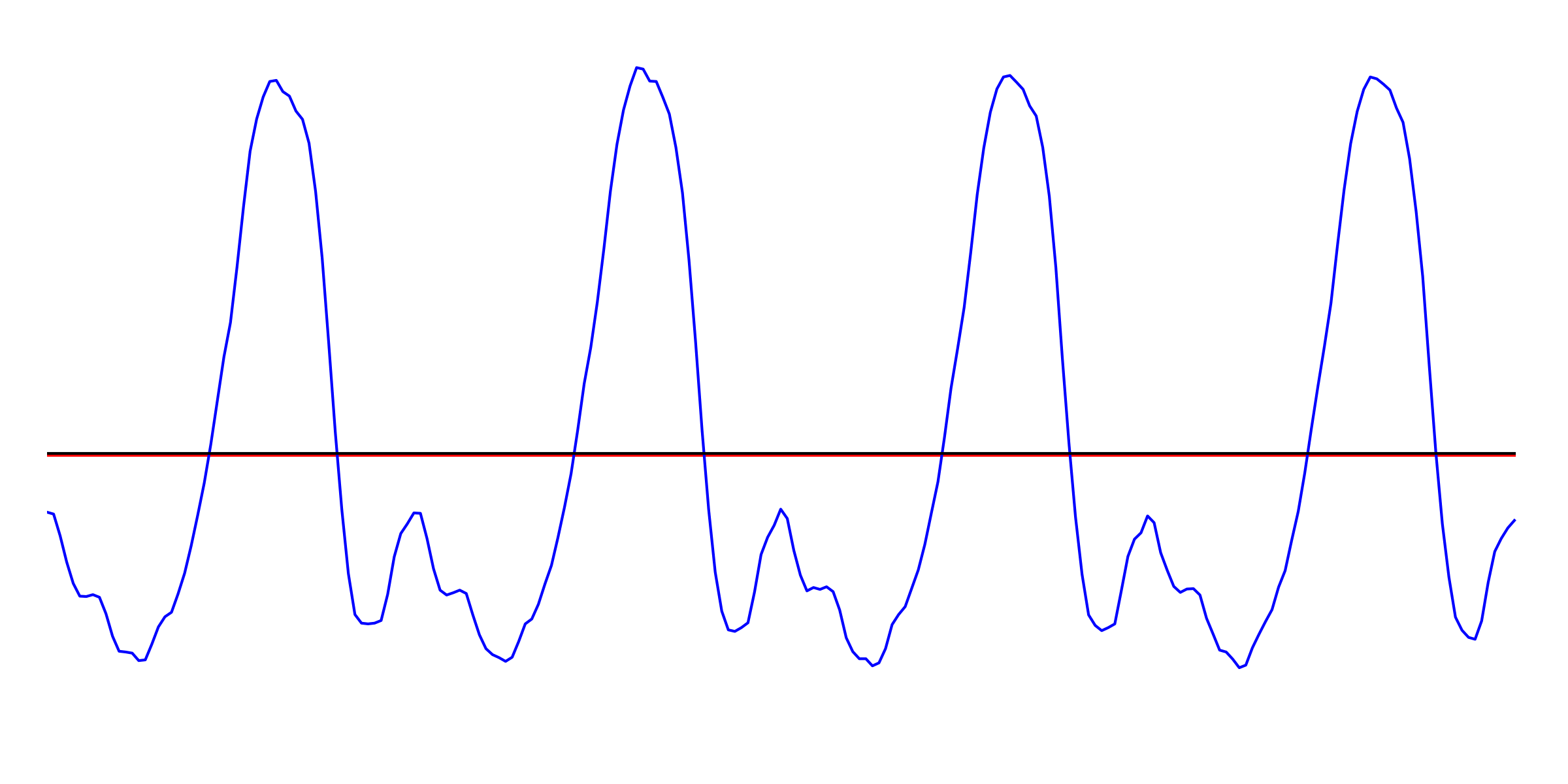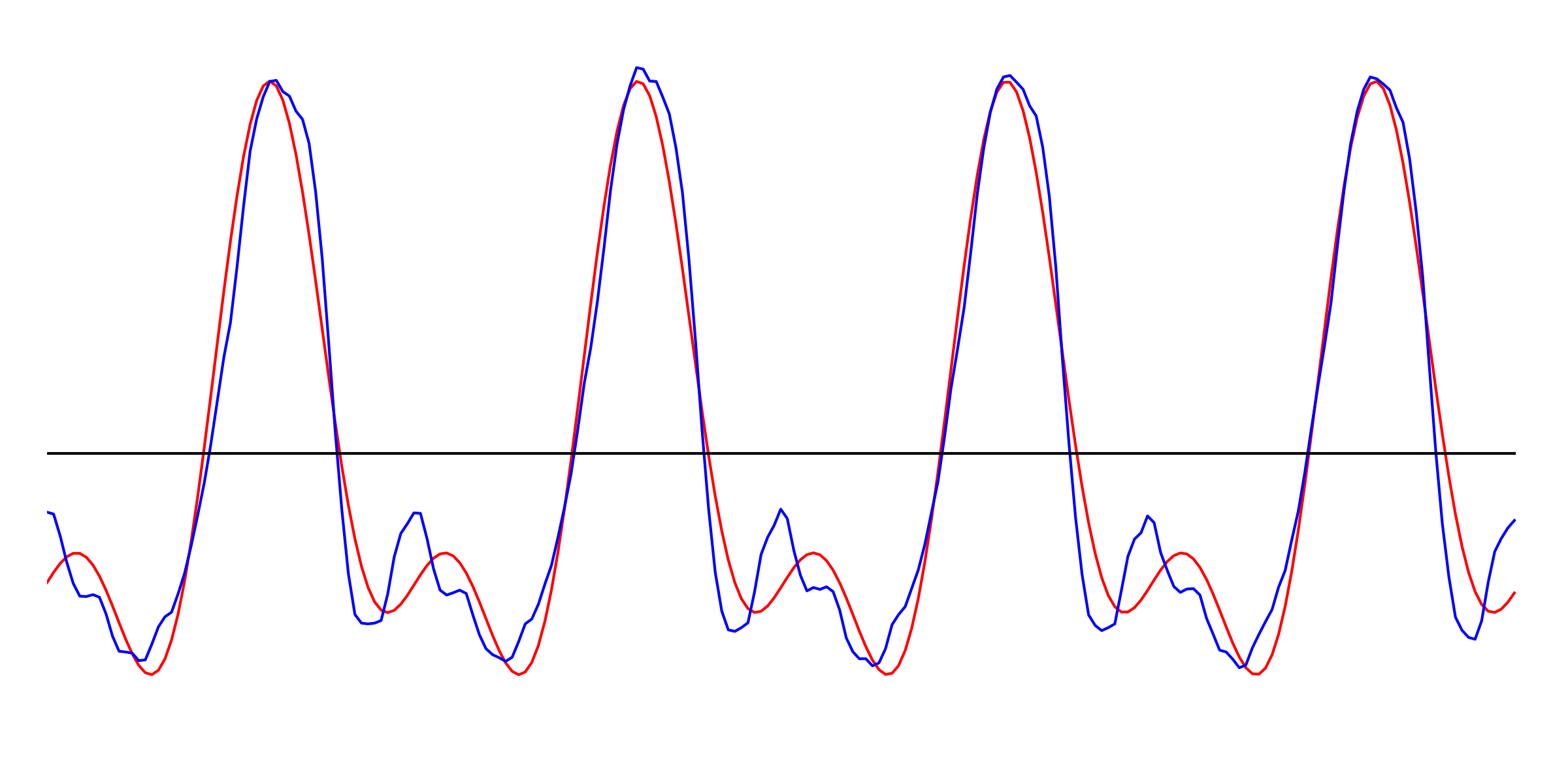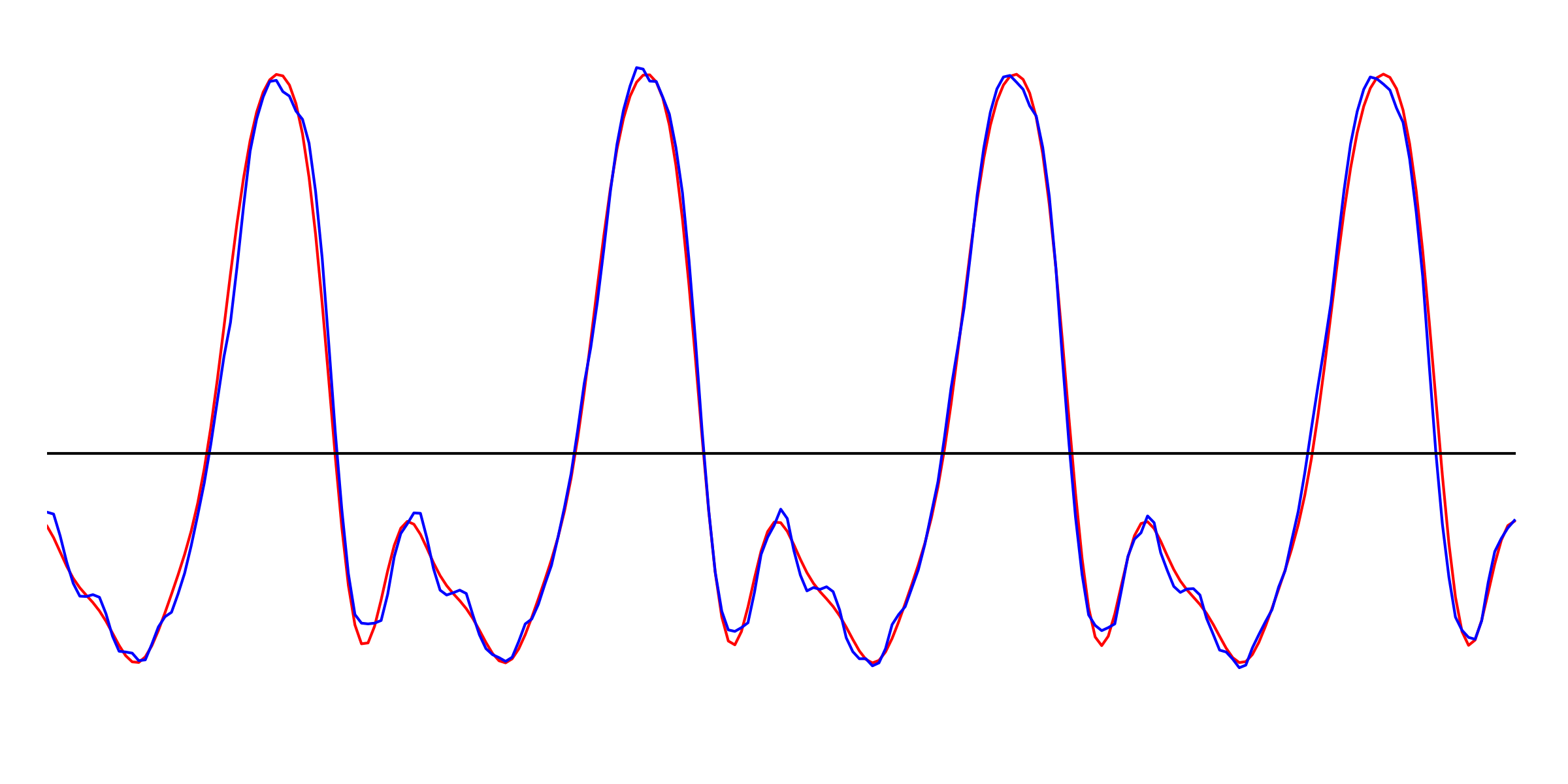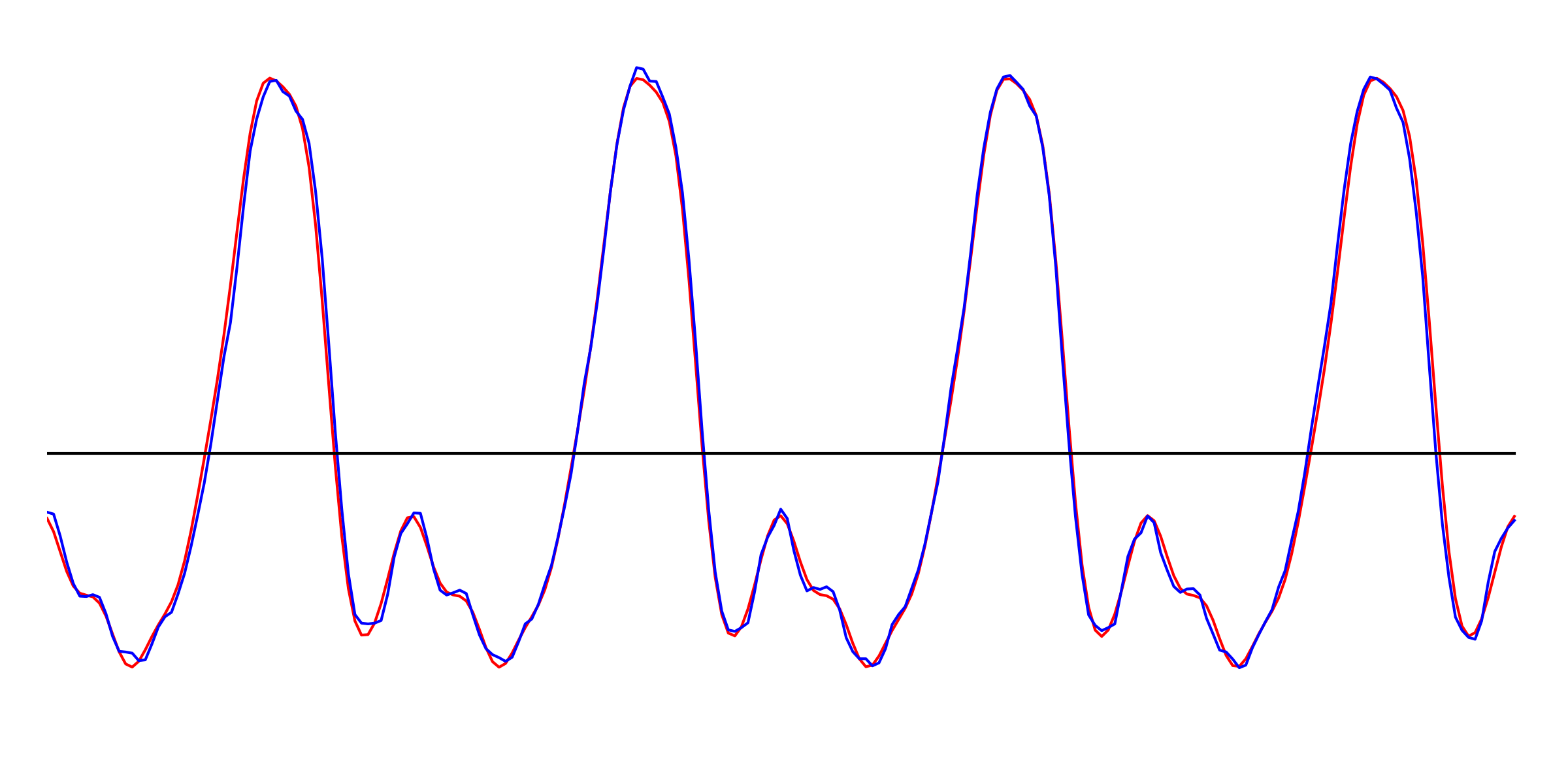
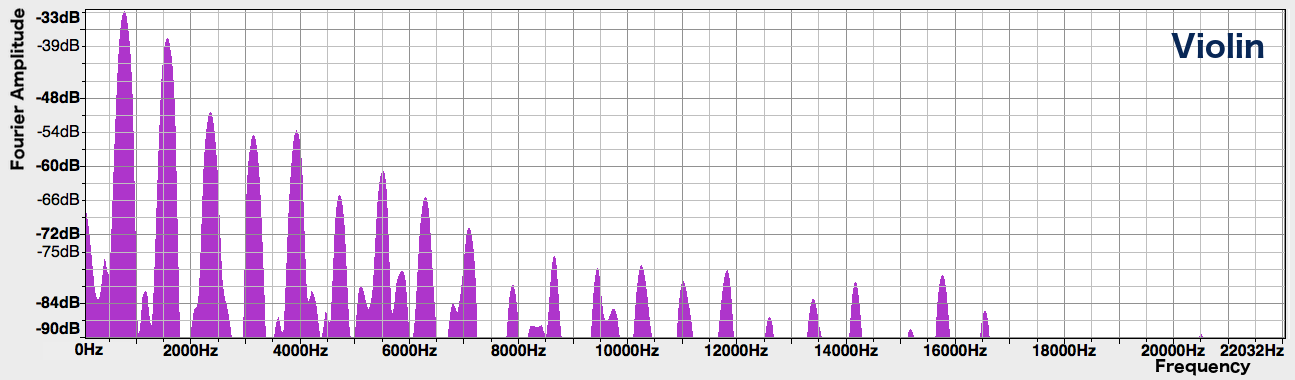
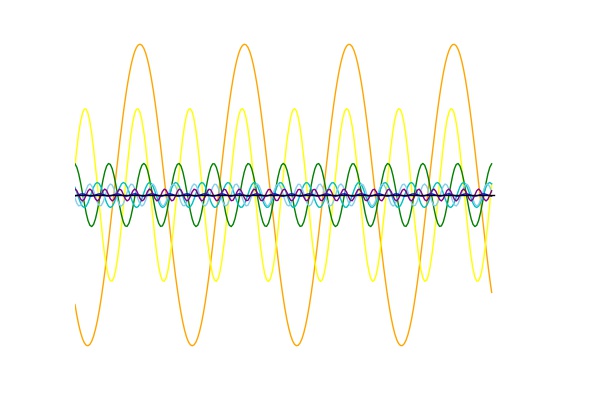
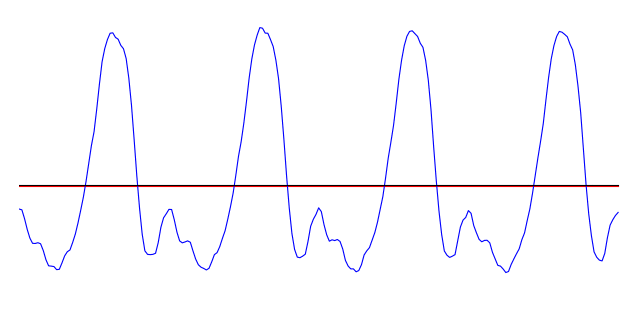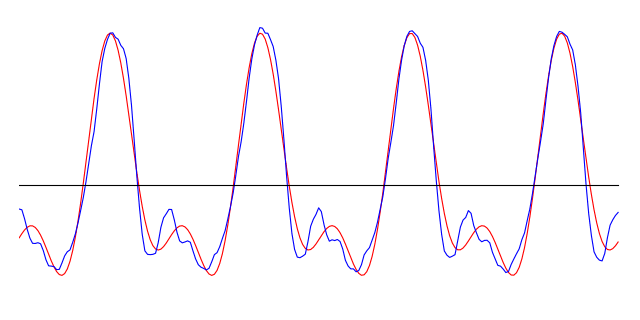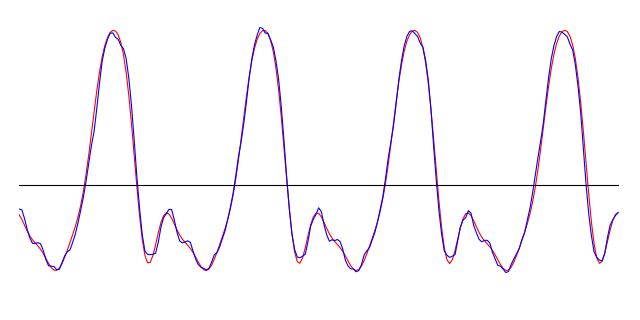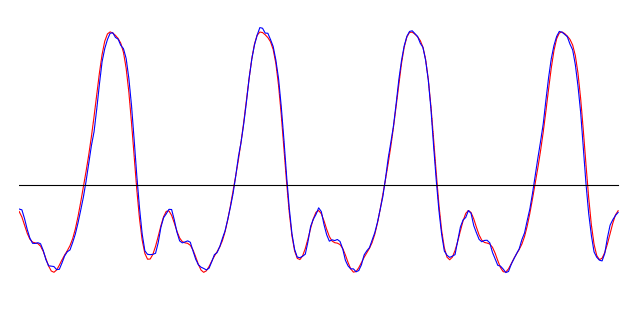
Click to expand: Sine waves and outer space

The Fourier Theorem: Everything is Made of Sine Waves

So why are sine waves useful to us?  It turns out that there is a mathematical theorem called the Fourier theorem, which says that you can take any periodic waveform and break it down into a whole bunch of sine waves of different frequencies.  Conversely, if you take the correct amounts of sine waves of each frequency, you can add them up to get the original waveform.  In a sense, sine waves act like building blocks from which you can get any complicated periodic waveform you want. 

Let’s go back to the spectrum of a sound.  If the spectrum has a peak at, say, 1568 Hz, it means that when you break the sound down into sine waves, there is a particularly large contribution from the sine wave that has a frequency of 1568 Hz.

Now have a look at the spectrum of the above violin note.  The spectrum’s distinct peaks indicate the fundamental frequency of 784 Hz and its harmonics.  The following image shows the sine waves that have frequencies and amplitudes corresponding to the first 7 peaks (each one has been shifted along the x-axis by some amount, to ensure that they add up correctly later).  Notice that the higher-frequency sine waves have lower amplitudes or heights, corresponding to the diminishing height of the spectral peaks at higher frequencies.

These first few harmonics are the strongest components that make up the violin sound.  In the following animation, the red line shows the resulting sum when we start from the first sine wave (with f = 784 Hz), and successively add in the sine waves corresponding to the next 9 harmonics.  As we add each successive sine wave, the sum approaches the original signal (in blue) more and more closely.  You can also hear the resulting sound, which starts from a pure sinusoidal tone at the fundamental frequency, and sounds more and more like a violin as more harmonics are added in.

Click to expand: More details

Jagged Waveforms

Even waveforms that don’t look smooth can be broken down into sinusoidal components.  Take the sawtooth wave that we saw above, for instance.  This is a jagged periodic wave, so-named because its shape resembles the edge of a saw:

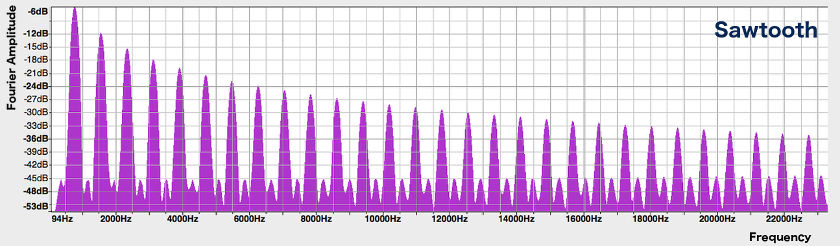
This computer-generated sawtooth wave has a frequency of 784 Hz, equal to that of our violin note above, but its spectrum shows high-frequency peaks that are much stronger.  This animation shows how the sawtooth waveform is approximated by the sine waves corresponding to the fundamental and first 49 harmonics:

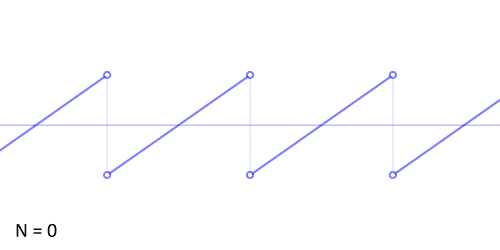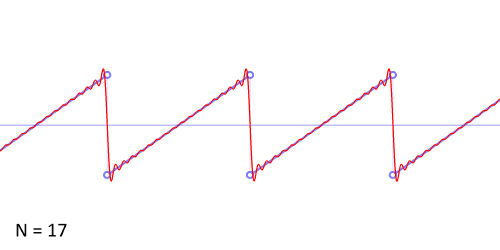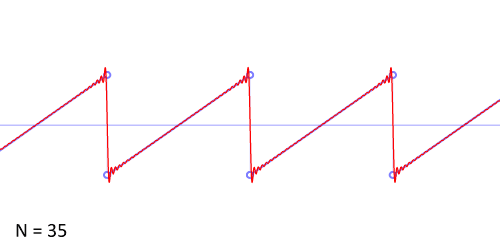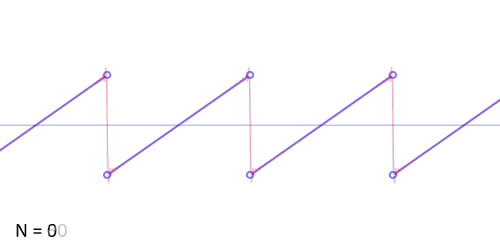
While the sum approaches the sawtooth shape very closely, we don’t quite get there – since the sine waves are smooth, they have a lot of trouble forming the sharp corners of the sawtooth.  In order to get back the sawtooth wave exactly, we would need to add an infinite number of sine waves, of increasingly higher frequencies.  Unlike the natural sounds of the flute and violin, the sawtooth’s harmonics don’t die out quickly as we get to higher and higher frequencies.  The strength of its high harmonics gives the sawtooth a very abrasive sound, though you can still hear its distinct G pitch.  Generally, waveforms with sharp corners (not often seen in physical instruments) have lots of high harmonics, and sound harsh.