The Kinkiness of a Vibrating String

Here’s a super-slow-motion video of a vibrating violin string:

Video by Jost Fischer.

I think this is pretty cool — there’s this kink that’s travelling up and down the length of the string.  What’s going on here, and why don’t we see this with the naked eye?  In this post I’ll explain how a bowed string vibrates, and how, unintuitive as it seems, the odd kinky motion of the string can be produced from simple sine waves.

Have a look at this animation of the bowing process:

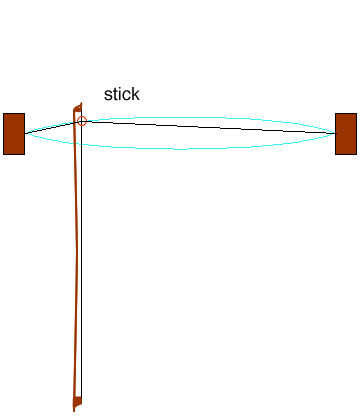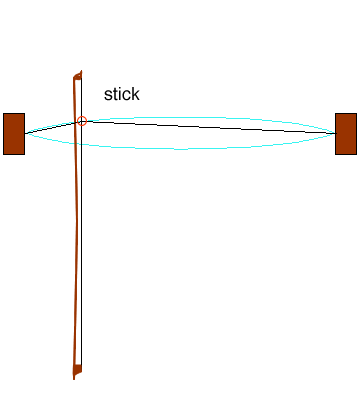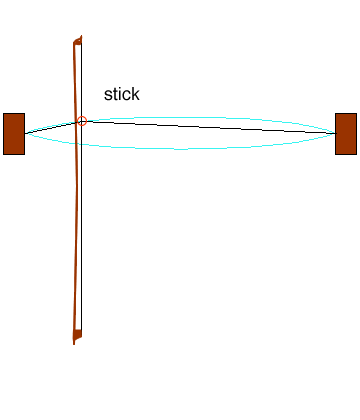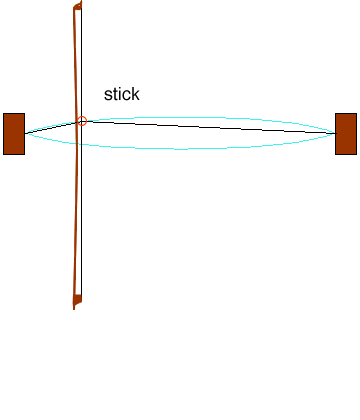
There’s quite a bit going on here, so let’s try to break it down.  First, notice that the kink, as it races up and down the string, traces out a curve (marked in cyan).  This sort of eye-shaped envelope is what we see when we look at a vibrating string, because our eyes aren’t fast enough to pick out the kink.

Secondly, you might also have noticed the words “stick” and “slip” appearing on the animation.  These refer to how the bow is interacting with the string.  A violin’s bow, usually made of horsehair, is coated with something called rosin.  This is a sticky substance made from pine resin that comes in little blocks wrapped in a cloth, and which the musician rubs onto the bow before each playing session.  The sticky powder creates friction between the bow and string, which is vital for the instrument to work properly.

Here’s how the bowing process works: When the string is undisturbed, it is perfectly straight, and quite taut.  When the rosined bow touches the string and moves upwards (as in the animation), it grabs onto the string and pulls it away from its equilibrium (undisturbed) position.  But the string can only be pulled so far upwards, before it slips and tries to go back to being straight.  It overshoots its equilibrium position and starts to bend the other way, and then the bow grips on to it once more, dragging it again upwards.  This stick-slip cycle repeats several hundred times per second.

We can see from the animation that the stick-slip cycle is synchronised with the movement of the kink up and down the string.  The majority of each cycle is spent in sticking mode, with the string moving in the same direction as the bow; the slipping happens much more quickly.  Each time the kink passes under the bow, it triggers a change from sticking to slipping, or vice-versa.

Standing Waves

In a previous post, we looked at the Fourier theorem, which says that any periodic wave can be broken down into sine waves with frequencies that are integer multiples of some fundamental frequency.  The kink travelling up and down the string is a wave, too — what do its component sine waves look like?

The part of the string that can vibrate lies between two anchor points, called the bridge and the nut:

Since the string can’t move at those points, we’d expect the sine waves on the string to look like this:

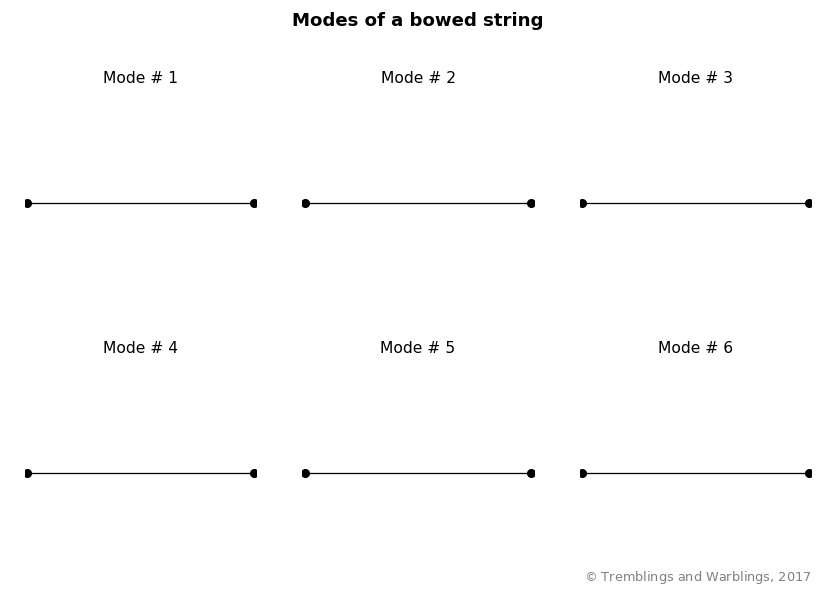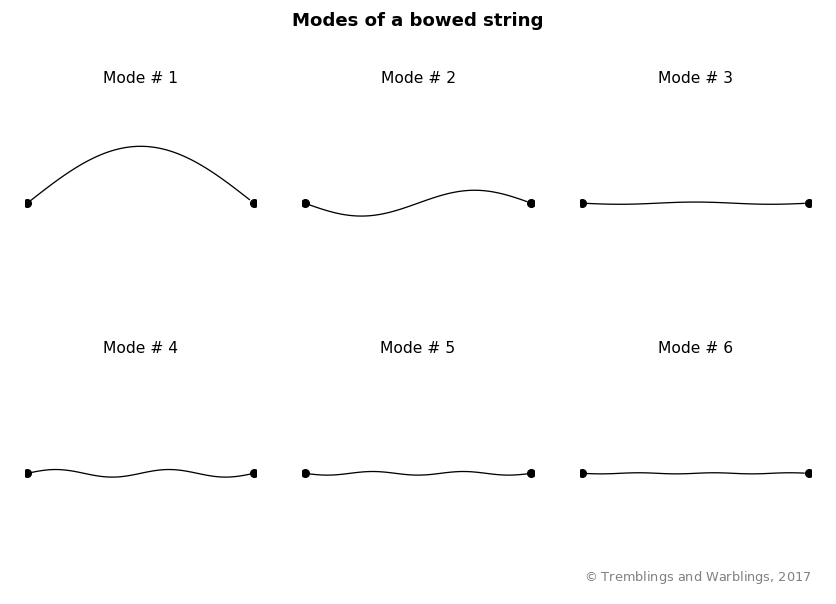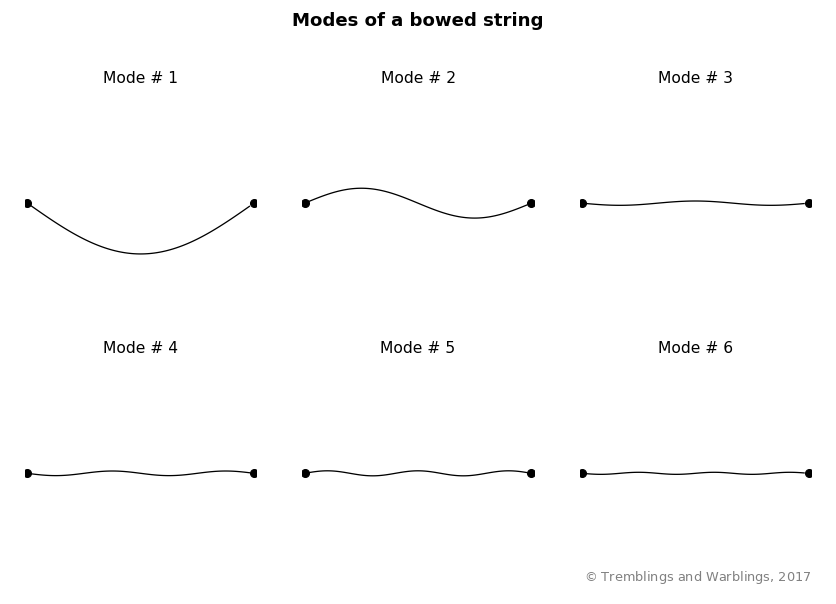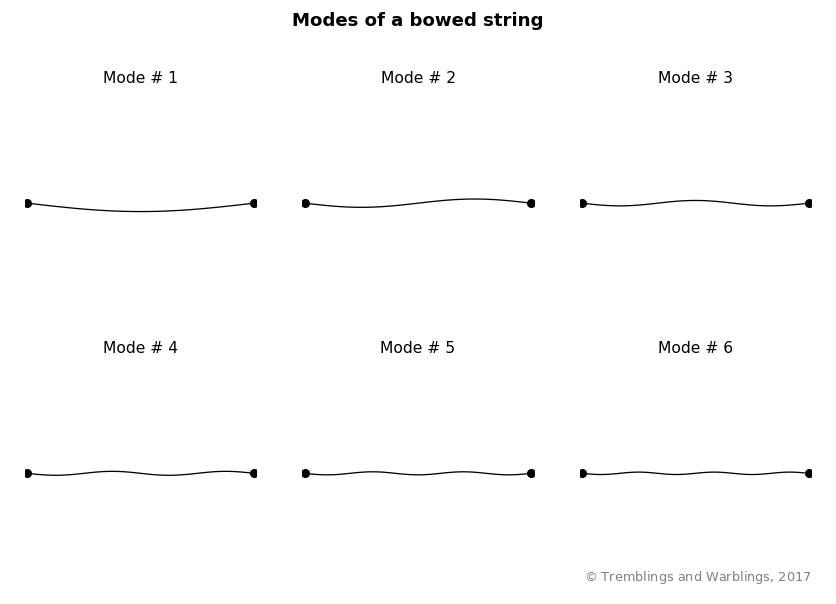
These waves are standing waves, which means that they don’t travel up and down the string — they just waggle the string back and forth.  Each of these different sine waves is called a mode of the string’s vibration.  The first mode traces out one eye-shaped envelope between the fixed anchors; the second mode traces out two, and so on.  From the second mode onwards, there are points on the string (between adjacent eye shapes) where it doesn’t move, even though those points are not physically restrained by anything.  These points are called nodes.

Notice that all the modes are vibrating at different frequencies, with the higher modes vibrating more rapidly.  Also, the lower modes have a larger amplitude — they bend the string by a larger amount.

Now watch the following animation, which starts with the first mode and then adds in successive modes.  As the modes combine, something magical happens:

Even though each individual mode is a standing wave that doesn’t move along the string, adding them together somehow forms a wave that does travel up and down.  This is because the modes each have different frequencies, so that at any one time, each mode is at a different part of its cycle compared to other modes.  This has the effect of making their sum look quite different from the individual modes.

Click to Expand: Mode Frequencies

Plucked Strings

So far we’ve mostly been talking about bowed strings, but it turns out that plucked strings also involve travelling kinks:

Motion of Plucked String by Dan Russell.

Notice, though, that this kink has a different shape from that of the bowed violin string — this one even seems to bounce back and forth.  The nice thing is that we can obtain this different shape of kink using the same sine wave modes as the violin kink.  We just need to use a different recipe for the mode amplitudes and phases.

The phase of a repeating wave (like a sine wave) tells us where in the cycle the wave happens to be at any one time.  If two waves are out of phase, it means that one of them is going up whenever the other is going down, and vice versa.

The shape of the guitar string kink depends on the point on the string where it is plucked.  If we pluck it, say, one fifth of the way along the string, then every mode that is a multiple of 5 will be suppressed (since it would have had a node at the plucking location).  We would also have to flip the phase for each group of five successive modes (so modes 1-4 have the same phase, modes 6-9 have the opposite phase, modes 11-14 have the same phase as modes 1-4, and so on).  The result looks like this:

(In the video of the real plucked string, the kink decays over time.  For simplicity’s sake I didn’t take this decay into account in the animation.)

A Rich Spectrum

In most stringed instruments, the vibrations of the string are transferred to the instrument body via the bridge, a piece of wood wedged between the string and the body.  The body, in turn, plays an important role in shaping the instrument’s sound, by filtering the spectrum of the vibrating string. 

In an earlier post, we saw that waveforms with sharp corners usually have a lot of strong high harmonics — our kink is no exception.  The presence of all these harmonics in the string’s vibration gives the instrument body more “raw material” to work with as it applies its filtering effect.

In a future post, I’ll talk about the role of the instrument body in more detail.  I’ll compare two stringed instruments that have a similar size but very different body shapes, and that happen to come from two different musical cultures: the violin and the erhu.